L'Ultimate Texas Hold'em (UTH) è uno dei nuovi giochi più popolari nel mercato. E per questa ragione è importante capire i molti modi in cui l'UTH può essere vulnerabile, adottando la tattica dell'advantage play e quali sono le differenze con l'Heads-Up Hold'em!
Molti dei miei post più recenti hanno riguardato alcune di queste possibilità. Ma le computazioni rischiano di apparire noiose. Ci sono voluti ben cinque giorni, infatti, al mio computer per finalizzare il ciclo in cui l'AP vede una delle carte coperte del mazziere. Poi il mio computer ha trascorso otto giorni ad analizzare la situazione in cui l'AP vede una carta coperta del mazziere e una carta del flop.
E dopo ancora, il mio computer ha lavorato per poco più di due giorni considerando ragionamenti perfetti con sei giocatori al tavolo. Dopo tutto questo tempo passato a ragionare di advantage play, ho deciso di fare un passo indietro e di calcolare il vantaggio del banco a livello generale, usando una strategia di base perfetta, ma senza tattiche di advanced play.
Attenzione: al mio computer ci sono voluti altri tre giorni per calcolare il ciclo del preflop e altri due per calcolare quello del flop. Ma alla fine ho qualche dato di strategia da presentare.
Doveroso evidenziare che questa analisi è già stata presentata (ed è stata fatta meglio) sia da Michael Shackleford che da James Grosjean. In particolare, la straordinaria ricerca di Michael Shackleford sull'UTH include una strategia pratica per il flop (check / raise 2x) e per Turn/River (raise 1x / fold), che io utilizzerò in questa presentazione.
Alla luce di quello che è già stato fatto prima, se non avrò nulla di nuovo da aggiungere non lo farò in questa sede.
Ma, come potranno vedere presto i lettori, questo lavoro, oltre a conoscere le regole Ultimate Texas Holdem include parecchi megabyte di divertimento.
Tanto per ricordarvele, ecco le regole su come vincere al casinò con l'UTH:
1. Il giocatore fa puntate uguali sulla Ante e sulla Blind.
2. Vengono date cinque carte comuni a faccia in giù al centro del tavolo.
3. Il mazziere dà a se stesso e a ogni giocatore due carte iniziali a faccia in giù.
4. Ora i giocatori hanno una scelta:
1. Fare check (quindi non fare nulla), oppure
2. Effettuare una puntata di 3x o 4x rispetto alla loro ante.
5. A quel punto il mazziere rivela le prime tre carte comuni (le carte del "flop").
6. I giocatori che non hanno ancora puntato hanno una scelta:
1. Fare check, oppure.
2. Giocare una puntata di 2x rispetto alla loro ante
7. Il mazziere rivela le due carte comuni finali (le carte del Turn/River)
8. I giocatori che non hanno ancora fatto una puntata hanno un'opzione:
1. Foldare e lasciare l'Ante e la Blind, oppure
2. Fare una puntata uguale alla Ante.
9. Il mazziere rivela le sue carte iniziali e annuncia la sua mano migliore da cinque carte. Il mazziere ha bisogno di una coppia o di una mano migliore per "qualificarsi".
E ora, che succede? Beh, o il mazziere si qualifica oppure no. Il giocatore batte, pareggia o perde rispetto al mazziere. O la mano del giocatore è abbastanza buona per qualificarsi per una vincita bonus sulle Blind, oppure non lo è.
La seguente tabella dovrebbe (si spera) chiarire tutte queste possibilità e segnalare la vincita in ognuno dei casi.
| Mano vincente | Il mazziere si qualifica? | La Ante paga | La puntata paga | La Blind paga |
| Giocatore | Sì | 1 a 1 | 1 a 1 | Vinta |
| Giocatore | No | Pari | 1 a 1 | Vinta |
| Mazziere | Sì | Persa | Persa | Persa |
| Mazziere | No | Pari | Persa | Persa |
| Pareggio | Qualsiasi risultato | Pareggio | Pareggio | Pareggio |
Il pezzo finale del puzzle è la puntata blind. Come mostra la tabella qui sopra, se il giocatore vince la mano, indipendentemente dal fatto che il mazziere si sia qualificato oppure no, la puntata blind del giocatore viene pagata al casinò secondo la seguente tabella di vincita.
- La Scala Reale paga 500-a-1.
- La scala colore paga 50-a-1.
- Il poker paga 10-a-1.
- Il full paga 3-a-1.
- Il colore paga 3-a-2.
- La scala paga 1-a-1.
- Tutte le altre mani pareggiano.
Analisi combinatoria
I miei appunti di calcolo che contengono l'analisi combinatoria completa, che presenta le 169 mani iniziali uniche possibili, assieme al vantaggio sul check e sul raise 4x.
Il foglio di calcolo dà anche il numero di mani equivalenti a quelle nella lista (le permutazioni per seme). PEr esempio, visto che la mano iniziale (2c,7d) è equivalente a (2h, 7s), solo la mano (2c,7d) è stata analizzata.
Così, in particolare:
- Il vantaggio del banco nell'UTH è del 2,18497%.
- Il giocatore fa check nel pre-flop nel 62,29261% delle mani.
- Il giocatore fa raise 4x nel pre-flop nel 37,70739% delle mani.
- Il giocatore ha un vantaggio nei confronti del banco nel pre-flop nel 35,29412% delle mani.
- Il giocatore non dovrebbe mai fare raise 3x nel pre-flop.
Strategia per il Pre-Flop
Ecco un riassunto della strategia di base nel pre-flop presa dal foglio di calcolo inserito sopra e valida anche per il casinò live!
- Raise 4x sulle seguenti mani, che siano dello stesso seme oppure no:
- da A/2 a A/K
- da K/5 a K/Q
- da Q/8 a Q/J
- J/T
- Raise 4x sulle seguenti mani dello stesso seme:
- K/2, K/3, K/4
- Q/6, Q/7
- J/8, J/9
- Raise su ogni coppia di 3 o più alta.
- Check su tutte le altre mani
Strategia per il Flop
La decisione di fare check o raise 2x al flop è possibile solo se il giocatore ha fatto check nel pre-flop.
Facendo riferimento alla strategia per il pre-flop descritta sopra, rimangono esattamente 100 classi equivalenti di mani iniziali in cui il giocatore ha fatto check nel pre-flop. Ho fatto di nuovo partire il mio programma per la strategia di base dell’UTH per considerare ognuna di queste 100 mani e ogni possibile flop che può uscire con quella mano iniziale.
Per ogni mano iniziale in cui il giocatore ha fatto check nel pre-flop, ci sono 19.600 flop da considerare. Quindi, in totale, ho dovuto valutare la decisione se fare check o raise 2x nel flop per 100 x 19.600 = 1.960.000 situazioni.
Ho lavorato su quattro fogli di calcolo che contengono l’analisi per ognuna di queste 1.960.000 possibilità. Ogni foglio di calcolo ha i dati totali per 25 mani iniziali del giocatore. Nota, ognuno di questi fogli di calcolo pesa circa 20 megabyte.
Per comprendere i dati in questi fogli di calcolo, l’immagine che segue dà le prime decisioni al flop per la mano di partenza (8c, Jd) (vedi foglio di calcolo numero 3)
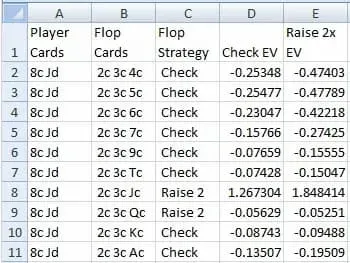
Per esempio, considerando la mano del giocatore = (8c, Jd) e il flop = (2c, 3c, Jc), l’EV per il check è di 1,267304, mentre l’EX per fare raise 2x è di 1,848414. Come è intuitivamente ovvio (visto che il giocatore ha una coppia di Jack), la mossa esatta in questa situazione è fare raise 2x.
Ora date un’occhiata alla mano sotto, giocatore = (8c, Jd) e Flop = (2c, 3c, Qc). Anche questa è una mano in cui il giocatore dovrebbe fare raise 2x (le due decisioni sono molto vicine), ma non capisco molto bene perchè dovrebbe essere così. Forse perchè c’è una possibilità di fare una scala o un colore con le ultime due carte.
Ora guardate la riga ancora successiva. Quando il giocatore ha (8c, Jd) e il Flop è (2c, 3c, Kc), allora bisogna fare check, perchè la possibilità di fare scala non c’è più.
Qualsiasi tentativo di quantificare questa serie di cambiamenti impercettibili in una strategia completa è sicuramente un compito faticoso. Il lettore è invitato ad analizzare i quattro fogli di calcolo (circa 80 mega) e a creare una strategia completa da solo. Io non mi sottoporrò a questo esercizio.
L’approssimazione di Michael Shackleford per la strategia nel flop è semplice e intelligente.
Il giocatore dovrebbe fare raise 2x con una doppia coppia o con una mano migliore, con una coppia nascosta (tranne che di 2) o con quattro carte per un colore con un kicker che sia un 10 o più alto.
Vediamo che la mano sopra, quella in cui il giocatore ha (8c, Jd) e il flop è (2c, 3c, Qc) viola la strategia di Shackleford, perchè sono quattro carte per un colore con come kicker 8c. La strategia non corretta di Shackleford per questa mano corrisponde a una perdita di EV molto piccola (0,377%). Ma questa piccola perdita di EV vale l’investimento, vista la semplicità strategica che porta.
Strategia per Turn/River
Come matematica applicata al casinò, si potrebbe anche usare la semplicissima strategia di Shackleford per la decisione finale al Turn/River: il giocatore dovrebbe fare raise 1x quando ha una coppia nascosta o quando ci sono meno di 21 carte rimaste per il mazziere che possono battere il giocatore, oppure dovrebbe foldare.
Si può anche usare la strategia più complessa di Grosjean, presa da Exhibit CAA, che non ripeterò qui. Buona fortuna se volete trovarne una copia. (James, rendi disponibili i tuoi libri, per favore!).
Il mio metodo completo, se dovessi crearlo, sarebbe quello di postare fogli di calcolo che contengono giocate perfette calcolate dal computer, in modo che sia il giocatore a sviluppare la sua strategia completa per il Turn/River.
Facendo riferimento alla strategia per il flop, delle 1.960.000 di possibilità sono 1.273.842 quelle che corrispondono a un check del giocatore al flop. Ognuna di queste possibilità ha un totale di 1.081 combinazioni al Turn/River per completare le carte in tavola, in cui il giocatore poi deve decidere se foldare o se fare raise 1x.
Quindi darvi il foglio di calcolo completo per la strategia nella decisione al Turn/River significherebbe postare un totale di 1.960.000 x 1.081 = 1.377.023.202 mani che il lettore deve considerare.
Sì, certo… in ogni caso, per i più curiosi, ecco la mia derivazione del risultato di Shackleford che riguarda le mani in cui ci sono 20 o meno carte rimaste che possono far vincere il mazziere.
Ovviamente se il giocatore folda il suo EV è di -2.
Poniamo che N sia il numero di carte rimaste in considerazione che permettono al mazziere di battere il giocatore. Quindi la probabilità che la prima carta del mazziere sia una di esse è di p = N/45.
Per la sua seconda carta, il mazziere che ha mancato la sua prima carta ha probabilmente altre 3 carte rimaste che gli fanno fare una coppia con la prima e battere il giocatore. Potrebbe anche generare nuove scale o colori (consideriamole come una carta rimasta addizionale). Quindi la probabilità che il mazziere batta il giocatore con la sua seconda carta è circa di (N + 4)/44.
In totale, la probabilità che il mazziere batta il giocatore è di
p = N/45 + [(45 - N)/45]*[(N + 4)/44].
Semplificando abbiamo:
p = (-N^2 + 85 N + 180)/(45*44)
Notate che se il mazziere non ottiene un punto con le carte rimaste, non si qualifica. E quindi l’EV per il giocatore che fa rimase 1x alla puntata del Turn/River è di :
EV = p*(-3) + (1-p)*(1) = 1 - 4p.
Facciamo questo raise ogni volta che l’EV è minore di -2. Ovvero 1 - 4p > -2. Risolvere per trovare p dà
p
Ovvero il giocatore fa raise 1x quando la sua possibilità di battere il mazziere è del 25% o più alta.
Combinando le due espressioni con p, vediamo che l’EV è maggiore di -2 ogni volta che
(-N^2 + 85 N + 180)/(45*44)
Semplificando l’equazione,
N^2 - 85N + 1305 > 0
La soluzione dell’equazione dà come risultato
(1/2)*(85 + sqrt(2005)) = 64.9
(1/2)*(85 - sqrt(2005)) = 20.1
Affinché l’equazione di secondo grado sia positiva, N deve essere o più grande di entrambi i risultati o più piccolo di entrambi. Quindi N ≥ 65 o N ≤ 20. Il primo caso è una “soluzione impossibile”, il che porta alla conclusione che al massimo ci possono essere 20 carte per il mazziere per battere il giocatore.
Punti chiavi del vantaggio del banco nell'UTH
Questo è un sommario dei vantaggi del banco per le strategie di cui si è parlato sopra:
- una strategia perfetta, calcolata al computer, per l’UTH porta un vantaggio del banco del 2,18497%.
- La strategia più pratica di Shackleford per l’UTH porta un vantaggio del banco di circa il 2,43%.
- La strategia di Grosjean per l’UTH che si trova in Exhibit CAA porta un vantaggio del banco del 2,35%.


