Il “ritorno al giocatore” o RTP dei giochi da casinò è definito da:

Notate che questo numero è basato sulle vere puntate e sulle vere vincite. Non è il risultato di una computazione con un foglio di calcolo, facendo andare un ciclo o attraverso una lunga simulazione di gioco. L'RTP si basa su persone reali che fanno puntate in un casinò.
Per i giochi che non hanno strategia, come Casino War, il craps o la roulette di solito accade che:

In più, maggiore è il numero di volte in cui il gioco viene praticato, più l'RTP rappresenta informazioni sul vero ritorno del gioco, facendo diventare questa equazione sempre più "esatta".
Ma "esatta" non significa che le due parti si avvicinano sempre di più tra loro, bensì che il rapporto tra le due parti di questa equazione si avvicina sempre di più a 1 con il numero di partite che aumenta sempre più [100% – (vantaggio del banco)] / RTP > 1]
Il numero 100% – (vantaggio del banco) viene detto RTP teorico del gioco. A volte però la terminologia è abbastanza vaga e il valore 100% – (vantaggio del banco) viene definito l'RTP del gioco.
OSSERVIAMO INSIEME QUALCHE ESEMPIO
Per la roulette, l'RTP è 100% - 5,26% = 94,74%
Consideriamo un giocatore che sta giocando a craps e punta sulla linea del pass senza odds con un vantaggio del banco dell'1,41%.
Visto che nel craps non c'è strategia, l'RTP per la puntata sulla linea del pass è di 100% - 1,41% = 98,59%.
Invece per il video poker Jacks or Better con la tabella di vincita “9/6” l'RTP è 100% - 0,46% = 99,54%. Con la tabella di vincita “8/5”, l'RTP è 100% - 2,70% = 97,30%.
Le slot molto generose hanno un RTP superiore al 96%. Quelle che pagano meno hanno un RTP inferiore al 92%.
Esaminiamo adesso il caso delle lotterie e cerchiamo di studiarne l'RTP. Poniamo che in ogni lotteria ci sia un milione di biglietti. Premettiamo anche che tutti quanti i biglietti siano stati comprati, in questo modo la cifra puntata è di un milione di euro.
La cifra totale vinta dai giocatori è di 900mila euro, o 900mila biglietti che pagano un euro ciascuno o 9 biglietti che ne pagano 100mila ciascuno.
Quindi, facendo un ciclo completo, l'RTP è:

Immaginiamo ora, amici lettori, di offrire la lotteria numero 2 e di vendere 500mila biglietti. Quindi il totale puntato è di 500mila euro. Sappiamo che esattamente il 90% di quei biglietti è vincente. Quindi, basandoci sul fatto che conosciamo il vantaggio del banco, ci aspettiamo che i giocatori vincano circa il 90% di 500mila euro, quindi 450mila.
Lo stato ha una vincita teorica di 50mila euro, che definiamo aggio. Per la lotteria 2 questo incasso è abbastanza certo a causa dell'alta frequenza di vincita (del 90%) e della vincita bassa dei biglietti vincenti.
L'RTP teorico a quel punto si trasferisce in risultati abbastanza precisi nel mondo reale.
Ora, poniamo di offrire la lotteria 1 e di vendere 500mila biglietti. Anche stavolta la cifra totale puntata è di 500mila euro. Ci sono solo 9 biglietti vincenti tra il milione di biglietti, quindi verrà venduto un numero di biglietti vincenti che va da 0 a 9.
La probabilità maggiore è che vengano venduti 4 o 5 biglietti vincenti, mentre è meno probabile che ne vengano venduti 3 o 6 e così via, con il caso più improbabile che è quello in cui ne vengono venduti 0 oppure 9.
Basandoci sul vantaggio del banco del 10%, ci aspettiamo che i giocatori vincano circa il 90% di 500mila dollari, quindi 450mila. Siccome i biglietti vincenti valgono tutti 100mila euro e ce ne sono solo 9, i giocatori in realtà vincono qualche centinaio di migliaia di dollari, da 0 a 900mila.
Il caso più probabile è che ne vincano 400mila o 500mila (con 4 o 5 biglietti vincenti venduti). Non c'è modo di vincere il 90% di quei 500mila euro. Se vendiamo 4 biglietti vincenti l'RTP è (400.000 €) / (500.000 €) = 80%. Se ne vendiamo 5, l'RTP è (500.000 €) / (500.000 €) = 100%. Non potremo mai avere un RTP del 90% se vendiamo esattamente 500mila biglietti.
Consideriamo ora dei veri esempi da casinò live. Se il giocatore lancia un milione di volte i dadi a craps puntando sulla linea del pass e punta un euro ogni volta, alla fine di questo milione di round avrà puntato un milione di euro.
Il giocatore ha "teoricamente" vinto una cifra che si avvicina a 985,900 euro di quelli puntati. E visto che vincere o perdere sulla linea del pass ha la stessa possibilità di avvenire, si può prevedere che la vincita reale e quella teorica siano abbastanza vicine, quindi l'RTP dovrebbe essere abbastanza vicino al 98,59%.
Più si gioca al gioco, più vicino l'RTP della puntata sulla linea del pass sarà vicino al 98.59%.
Poniamo che un giocatore di roulette punti un euro sul 7 rosso. In questa situazione, il vantaggio del banco è del 5,26%. Quindi ci aspettiamo che l'RTP sia circa del 94,74%. Se questo giocatore punta un euro sul 7 rosso per un milione di giri della roulette, alla fine avrà puntato un milione di euro e "in teoria" ne ha rivinti circa 947mila.
Ma siccome che esca il 7 rosso è un evento che non accade molto spesso (una volta su 38), è logico aspettarsi che la vincita reale e quella teorica del giocatore siano abbastanza diverse (come nella lotteria 1).
Poniamo vince che lo stesso giocatore punti quel milione di euro su "pari" invece che sul 7 rosso. In questo caso, visto che vincere o perdere sono cose che succedono quasi nella stessa quantità, l'RTP si avvicinerà velocemente verso il 94,74%.
Il punto è che l'RTP teorico dovrebbe essere abbastanza vicino al vero RTP per giochi che non prevedono strategia e in cui si vince spesso. Più raro è un evento vincente, più partite servono affinché questi due valori si avvicinino tra loro.
Nei giochi che hanno una strategia, i giocatori faranno errori. Per questo, il valore dell'RTP è spesso meno di 100 - (vantaggio del banco).
Per giochi con strategie semplici (come il Three Card Poker), l'RTP di solito è solo di poco inferiore a 100% – (vantaggio del banco). Per giochi più complicati, come il blackjack nella versione Switch o il Super Fun 21, l'RTP può essere al di sotto del valore teorico anche di parecchi punti percentuali.
Molti casinò sicuri (specialmente quelli online, in cui ogni interazione dei giocatori è registrata) creano rapporti mensili sull'RTP, in modo da poter calcolare la performance precisa di ogni gioco.
La figura 4 dà gli esempi di alcuni RTP mensili di un casinò online basato sul gioco dal vivo. Guardando con attenzione a questa tabella, possiamo fare alcune osservazioni.
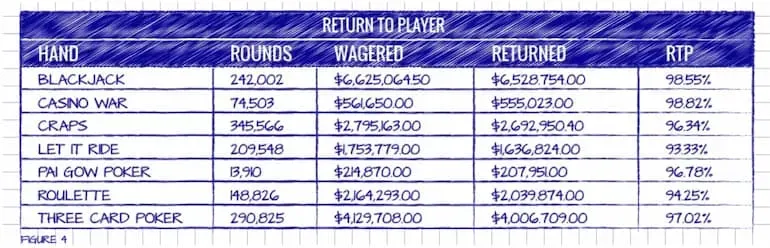
Notate che blackjack, Let it Ride, Pai Gow e Three Card Poker hanno tutti un ritorno inferiore all'RTP teorico che si ha con una strategia perfetta.
Basandoci sui risultati che dà la Figura 1, il blackjack ha un RTP teorico del 99,54%, Let it Ride ha un RTP teorico del 96,49%, il Pai Gow Poker ha un RTP teorico del 97,34% e il Three Card Poker ha un RTP teorico del 97.15%.
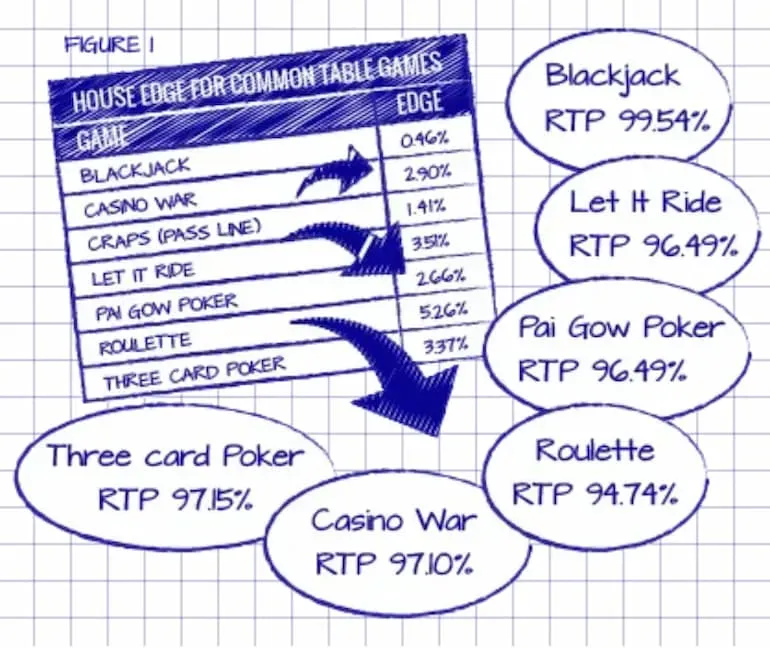
Dall'altro lato, Casino War è al di sopra dell'RTP teorico del 97,10% e la roulette si avvicina all'RTP teorico del 94,74%. Non è stato analizzato l'RTP per il craps a causa della varietà delle puntate disponibili.
Fate attenzione a un errore comune qui. Le carte, i dati, i rulli e le ruote non sanno quale RTP teorico dovrebbero avere e non provano ad arrivarci. Se l'RTP alla roulette è del 94,25% dopo 148.826 giri, non bisogna aspettarsi che il gioco cerchi di rifarsi nei 148.826 giri successivi in modo da avvicinarsi al valore teorico del 94,74%.
Se la linea del pass nel craps ha un ritorno del 102% non significa che i dadi sono destinati a raffreddarsi.
L'RTP reale non è un'indicazione di quello che succederà in futuro per colmare la differenza. O, come dicono nei fondi comuni o in altri tipi di investimenti, la performance in passato non dà indicazioni su possibili performance future.


