Una delle più comuni puntate secondarie per il blackjack nelle sale da gioco della California, ma non solo, è quella detta Buster Blackjack (BBJ).
Ho trovato questa testimonianza online. Il giocatore che fa la BBJ vince se il mazziere sballa. La vincita si basa poi sul numero di carte che compongono la mano con cui ha sballato.
Ci sono parecchi dettagli da vedere, quindi ho deciso di dividere la questione nel caso della partita a sei mazzi e quello della partita a due mazzi blackjack.
Questo articolo, in particolare, spiega il ruolo del conteggio delle carte nella puntata BBJ in una partita con sei mazzi.
Quando in una delle più importanti aziende bancarie statunitense, quindi gente che con i numeri ci lavora quotidianamente, mi hanno chiesto quali sono le vulnerabilità della BBJ al conteggio delle carte, io ho risposto loro “non molte”.
Dopo tutto, il mazziere ha bisogno di carte basse per generare mani con molte carte, ha bisogno di carte medie per fare totali di 15 o 16 e ha bisogno di carte alte per sballare.
La mia intuizione, in un certo senso, era sia giusta che sbagliata: la differenza sta nella tabella di vincita. Ci sono otto diverse tabelle di vincita per la puntata BBJ che vengono usate o che sono raccomandate.
Le ho studiate tutte e otto e ho scoperto che cinque sono vulnerabili mentre tre non lo sono.
Tanto per cominciare, mi concentrerò su una tabella di vincita della BBJ specifica e vulnerabile, Questa è una delle tabelle di vincita più comunemente utilizzate nelle stanze da gioco dei casinò.
La tabella di vincita è la seguente:
- se il mazziere sballa con 8 o più carte, la puntata paga 200 a 1;
- se il mazziere sballa con 7 carte, la puntata paga 100 a 1;
- se il mazziere sballa con 6 carte, la puntata paga 30 a 1;
- se il mazziere sballa con 5 carte, la puntata paga 6 a 1;
- se il mazziere sballa con 4 carte, la puntata paga 3 a 1;
- se il mazziere sballa con 3 carte, la puntata paga 1 a 1;
- altrimenti, il giocatore ha perso la sua puntata.
Ecco l’analisi combinatoria per questa tabella di vincita:
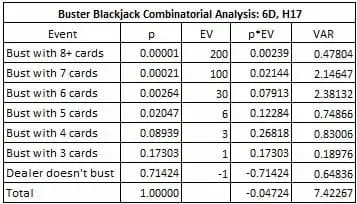
Scendendo ancor più nel particolare;
- il vantaggio del banco è del 4,724%.
- la deviazione standard è di 2,724;
- la frequenza con cui si vince è del 28,576%.
La tabella che segue dà l’effetto di rimozione (EOR) per ogni carta. L’EOR segnala il cambio nel vantaggio del banco dato dalla rimozione di una singola carta di un determinato valore e ricalcolando il vantaggio del banco.
Un EOR positivo significa che il vantaggio va verso il lato del giocatore togliendo la carta. Un EOR negativo significa che se la carta viene rimossa il vantaggio va dalla parte del banco.
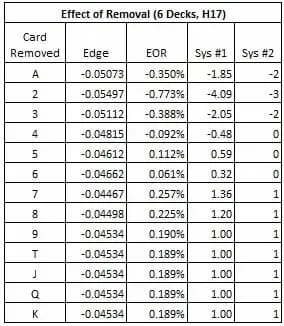
Notate quanto è più ampio l’EOR per le carte A, 2, 3 rispetto a tutte le altre. Quando ci sono parecchie di queste carte nel mazzo, è più probabile che il mazziere avrà mani con un numero maggiore di carte.
Che la mano del mazziere sballi oppure no non è importante per battere questa tabella di vincita: l’obiettivo primario è avere molte mani con più carte.
Togliere un singolo due da sei mazzi sposta il vantaggio verso il banco dello 0,77%, Ed è parecchio, In più un Asso non sballa mai con meno di quattro carte e rimuovere un Asso dai sei mazzi sposta il vantaggio verso il banco dello 0,35%.
Nella tabella qui sopra, sotto la colonna Sys #1, do dei valori per il conteggio delle carte con il sistema numero 1. Semplicemente uso l’EOR ridotto a due cifre decimali, proporzionato a seconda di una carta che vale 10 che ottiene un valore di 1. Il sistema numero 1 non è fatto per essere usato nella pratica, ma lo includo solo per determinare un limite massimo al profitto possibile contando le carte nella puntata BBJ.
Nella colonna Sys #2, vi do un sistema di conteggio delle carte bilanciato, che può essere usato nel gioco. Il sistema 2 mostra l’importanza delle carte A, 2, 3 per chi conta, con i due che sono le carte che valgono di più.
La correlazione di puntata per questo sistema è di 0,977. Per i patiti della matematica, questo valore è il coseno dell’angolo che si forma tra i vettori dati dal sistema 1 e dal sistema 2. Più questo valore si avvicina a 1, più preciso è il sistema.
Per analizzare questi due sistemi ho simulato cento milioni di contenitori da sei mazzi, con la carta per il taglio piazzata a 260 carte (ovvero a un mazzo dalla fine del mazzo) per ogni sistema. La tabella che segue riassume i risultati di queste simulazioni:
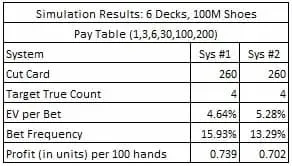
Notate che il sistema 2 fa tornare il 95% del profitto del sistema ottimale numero 1.
Questi numeri indicano una vulnerabilità moderata all’ interno di quello che definiamo advantage play con il conteggio carte blackjack.
Così, se l’AP usa il sistema 2 contro la puntata BBJ in una veloce partita uno contro uno in cui gioca 200 volte ogni ora e l’AP fa una puntata da 100 euro sulla BBJ ogni volta che ha il vantaggio, l’AP può guadagnare 140 euro all’ora sulla puntata secondaria BBJ. L’AP che usa il sistema 2 avrà un vantaggio medio nei confronti del banco del 5,28% e farà la puntata BBJ nel 13,29% delle mani giocate.
Come ho anticipato all’inizio dell’articolo, ci sono otto diverse tabelle di vincita per la BBJ che ho preso in considerazione. Questa tabella dà l’analisi combinatoria per un’altra tabella di vincita di uso comune:
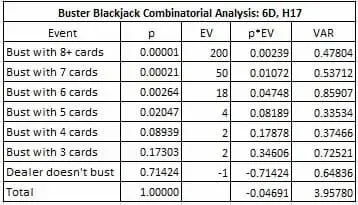
Andando sempre più a fondo nella nostra analisi;
- il vantaggio del banco è del 4,961%;
- la deviazione standard è di 1,989;
- la frequenza con cui si vince è del 28,576%.
Visto che una mano che contiene un Asso non può sballare, per la matematica applicata al casinò con meno di quattro carte, l’aumento della vincita che si ha quando il mazziere sballa con tre carte non entra in gioco con mani che includono un asso.
E in più, sballare con quattro o più parte ha vincite molto ridotte. Questi due fattori eliminano l’utilità degli Assi per chi conta le carte.
La tabella che segue dà l’EOR per questa tabella di vincita, assieme a un sistema di conteggio delle carte basato su questo EOR. Notate quanto cambia l’EOR per l’Asso.
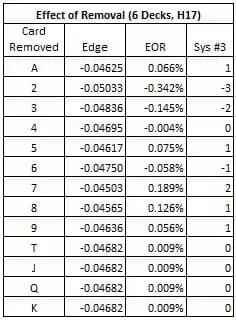
Il sistema #3 è una scelta ragionevole, basandosi sull’EOR. La correlazione di puntata per questo sistema è di 0,973.
Come quando ho proceduto nell'analisi della puntata secondaria baccarat DF 7, anche qui sono rimasto sorpreso nel vedere quanto sono diversi i valori di conteggio per questa tabella di vincita rispetto a quelli sviluppati per la tabella precedente. Questo sottolinea la profonda differenza nella strategia che serve per battere le due tipologie di tabella.
Non mi viene in mente nessun’altra puntata secondaria del blackjack che abbia un cambio di strategia così netto per l’AP basandosi solamente sulla tabella di vincita che viene utilizzata.
Per analizzare questa tabella di vincita e il sistema numero 3 ho elaborato una simulazione di venti milioni di contenitori da sei mazzi, con la carta per il taglio piazzata a 260 carte. E i risultati sono molto deludenti per chi fa advantage play.
- il conteggio che fa scattare la puntata è +8;
- il vantaggio medio è del 2,33%;
- la frequenza di puntata è del 3,64%;
- il numero di unità vinte per 100 mani è 0,085.
Questi numeri indicano una vulnerabilità molto bassa all’advantage play. Se il giocatore usa il sistema 3 in una partita veloce uno contro uno in cui riesce a giocare 200 round all’ora e se l’AP fa una puntata di 100 euro sulla BBJ ogni volta che ha il vantaggio, il giocatore in questione può guadagnare, di media, fino a 17 euro all’ora.
Ci sono altre due tabelle di vincita che sono simili a questa qui, che pagano 2, 2 e 4 unità quando il mazziere sballa rispettivamente con 3, 4 o 5 carte.
Le simulazioni che riguardano queste altre tabelle di vincita mostrano una vulnerabilità al conteggio delle carte ancora più basse. E quindi non includerò queste due tabelle di vincita in nessun’altra discussione sul conteggio delle carte contro la BBJ.
La tabella che segue riassume l’analisi combinatoria per sei diverse tabelle di vincita per la BBJ;
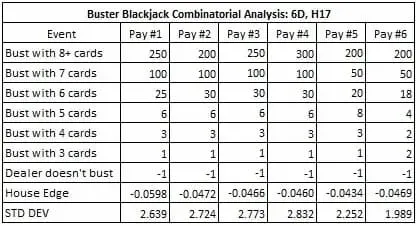
L'ultimo grafico, invece, dà i risultati del conteggio delle carte contro la BBJ in ognuna delle sei tabelle di vincita:
- per le tabelle #1, #2, #3, #4 e #5, ho usato il sistema #2, con valori (-2, -3, -2, 0, 0, 0, 1, 1, 1, 1);
- per la tabella #6 ho usato il sistema #3, con valori (1, -3, -2, 0, 1, -1, 2, 1, 1, 0).
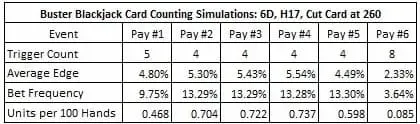
L’unica differenza tra le tabelle di vincita #2, #3 e #4 è la vincita maggiore. Per la tabella #4 l’AP può guadagnare circa 0,737 unità per 100 mani contando le carte contro la BBJ. Ed è un risultato che è il massimo a cui arriva un AP usando il sistema #2 in una partita a sei mazzi.
La debolezza relativa del conteggio delle carte usando il sistema #2 contro la tabella di vincita #5 mi ha sorpreso: pensavo avrebbe fatto meglio. Questi risultati possono dipendere dal fatto che il sistema #2 è stato creato per la tabella #2, magari un sistema di conteggio diverso funzionerebbe meglio contro la tabella #5.
Lascio la valutazione e lo sviluppo di questo sistema di conteggio a voi, come esercizio dopo aver letto.
Normalmente, a questo punto simulerei i vari livelli di penetrazione nel contenitore per dimostrare l’effetto del piazzamento della carta per il taglio per proteggere il gioco. E poi farei raccomandazioni per proteggere la BBJ che seguono un modello standard di protezione del gioco contro il conteggio delle carte nelle puntate secondarie del blackjack. Ma in questo caso, invece, è assolutamente chiaro come proteggere la BBJ.
Ho una sola ultima raccomandazione sulla BB per come vincere al casinò ed è davvero molto semplice:
- in una partita a sei mazzi, cercate solo versioni della BBJ con una tabella di vincita che paga 2 a 1 quando il mazziere sballa con 3 o 4 carte.


