Cos'è l'Expected Value nei giochi da casinò
L'Expected Value (valore atteso) è il valore medio a lungo termine delle ripetizioni dell'esperimento che rappresenta. Questo è quello che chiamiamo semplicemente "aspettative" e non ci dice se e quanto possiamo vincere o perdere su una specifica puntata in un gioco del casinò.
Nel gioco con Expected Value o Average Expectation intendiamo il calcolo di quanti soldi vinceremo o perderemo a lungo termine, basandoci sulle probabilità e sulle vincite del gioco. Ma vanno chiarite alcune cose:
1. La quantità di denaro che dovremmo aspettarci di vincere o di perdere di solito viene espressa con una percentuale rispetto ai soldi puntati.
2. Per "a lungo termine" intendiamo dopo molte migliaia di partite. Più se ne fanno, più ci si avvicina al valore della predizione dell'expected value.
3. Questa è una previsione teorica abbastanza precisa dei risultati a lungo termine del nostro gioco, ma comunque i risultati possono chiaramente variare.
Il vantaggio del banco nei giochi al casinò
Naturalmente, tutti i giochi del casinò hanno un valore di expected value negativo. Ci si aspetta che a lungo termine tutti i giocatori perdano, poiché i giochi sono creati a favore del casinò.
In realtà, l'expected value di ogni gioco del casinò è l'altro lato della medaglia (in maniera negativa) rispetto al vantaggio del banco: sono, in sostanza, la stessa cosa. In particolare, qui vi presentiamo l'expected value o vantaggio del banco dei principali giochi che si trovano al casinò:
- Roulette (doppio zero): -5,26%
Roulette (con un solo zero): -2,7%
Roulette (su puntate che pagano una volta la posta, con un solo zero e con regole La Partage o En Prison): -1,35%
- Blackjack: -0,5%.
- Caribbean Stud Poker: -5,22%.
- Craps, puntando su Don’t Pass: -1,36%.
Craps, puntando su Come: -1,41%
Craps, puntando sul pareggio
Craps, puntando su una coppia Pair: -10,36%
- Baccarat, puntando sul banco: -1,05%
Baccarat, puntando sul giocatore: -1,2%
- Video Poker: -1% (variabile, dipende dal gioco)
- Slot Machine: -10% (variabile, dipende dal gioco)
Questo expected value negativo (detto vantaggio del banco) è l'unica ragione per cui gli studiosi che analizzano la matematica applicata al casinò sostengono che sia impossibile vincere al gioco a lungo termine.
Ma, come ben ricordate amici lettori, ho spiegato in profondità le ragioni per cui non sono d'accordo con questa tesi nella mia monografia sul vantaggio del banco.
Come calcolare l'expected value di qualsiasi gioco e di qualsiasi puntata
Per la classificazione dei giochi per il margine, a volte ci possono essere regole speciali o magari non c'è un vantaggio del banco fisso. Ma potete sempre calcolare la probabilità e l'expected value (il vantaggio del banco negativo) di qualsiasi puntata usando la seguente equazione:
Expected value = (probabilità di vincere)*(profitto) + (probabilità di vincere)*(profitto)-(probabilità di perdere)*(valore della puntata) / valore della puntata
Se abbiamo più puntate allo stesso momento moltiplichiamo la probabilità che le nostre puntate vincono con il loro rispettivo profitto in caso di vittoria e le aggiungiamo assieme.
Poi togliamo la probabilità di perdere moltiplicata per la perdita (che è rappresentata dalla dimensione della nostra puntata). Poi dividiamo la somma per la dimensione della nostra puntata.
Se facciamo una sola puntata, allora l'equazione è:
Expected Value = (probabilità di vincere)*(profitto)-(probabilità di perdere)*(valore della puntata) / valore della puntata
Ora per rendere le cose ancora più semplici possiamo usare come dimensione di puntata una sola unità.
Se puntiamo di più o di meno, l'expected value sarà una frazione della nostra puntata, quindi diventa più semplice fare i calcoli se usiamo 1 (unità, fiche, euro, qualsiasi cosa) come nostro valore di puntata. In questo caso l'equazione diventa:
Expected value = (probabilità di vincere)*(profitto)-(probabilità di perdere)*(valore della puntata)
L'esempio con le dozzine
Ora calcoliamo l'expected value della puntata sulle dozzine nella roulette. Sappiamo già (vedi la sezione precedente) che ogni puntata alla roulette con un solo zero ha un expected value (o un vantaggio del banco) che è uguale a -2,7%, ma calcoliamolo per conto nostro.
Per una puntata sulla dozzina, la probabilità di vincere è di 12/37, perchè stiamo effettivamente puntando su 12 numeri su un totale di 37. Il profitto in caso di vincita è di 2 unità. La probabilità di perdere è 25/37, perchè 25 numeri su 37 ci fanno perdere. Quindi l'Expected value della puntata sulla dozzina è:
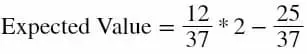
Che dà:
Il che significa che "a lungo termine" ci aspettiamo di perdere una cifra uguale al 2,7% del totale dei soldi che abbiamo puntato.
Un esempio da condividere
Una domanda dal nostro forum:
Poniamo che io stia giocando sui seguenti numeri: 1-2-3-4-5-6-7-8-9-10 e che io scommetta una sola fiche su ogni numero. Il croupier mi fa gli auguri per il compleanno e mi dice "puoi giocare altri due numeri in più senza dover pagare", quindi io aggiungo 11 e 12. Quindi ora sto giocando 12 numeri singoli al prezzo di 10. Quale sarebbe il mio vantaggio?
Calcoliamo l'expected value di questo esempio di fantasia. Puntiamo su 12 numeri con sole 10 fiches e ogni numero ci paga un profitto di 35 unità. Quindi abbiamo:
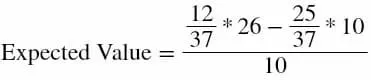
Che dà:
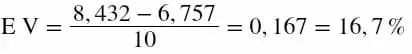
Quindi invece di avere uno svantaggio del -2,7%, in questo particolare esempio abbiamo un vantaggio del 16.7%.
Attraverso l'equazione descritta in questo articolo potete calcolare il vantaggio o lo svantaggio di qualsiasi puntata casuale, se sapete quali sono le probabilità di vincere.


