Comprendere le statistiche utilizzate dai casinò è fondamentale per valutare i propri risultati al tavolo da gioco.
Noi le utilizziamo per capire se i nostri risultati, che siano buoni o cattivi, arrivati grazie l'abilità oppure semplicemente per fortuna.
In questo articolo ci concentriamo per l’analisi statistica al blackjack, ma lo stesso ragionamento può essere mutuato per qualsiasi gioco del casinò con uno sforzo davvero minimo.
Partiamo dal dire che il blackjack non sposa, per definizione, le classiche leggi matematiche del gioco.
Quasi tutti i giochi che si basano sul caso riflettono quel concetto matematico conosciuto come “la legge degli eventi indipendenti”, il quale sostiene che gli eventi avvenuti in passato non hanno alcuna rilevanza su quelli che avverranno in futuro.
Se viene lanciata una moneta, c’è un 50% di possibilità che il risultato sia testa e un 50% di possibilità che il risultato sia croce. Anche se nel lancio della moneta esce testa 10 volte consecutive, nel prossimo lancio ci sarà comunque un 50% di possibilità che esca di nuovo testa.
Nel blackjack invece quello che accade in passato ha, evidentemente, un effetto diretto su quello che accade nel futuro. Il blackjack ha una memoria e la “legge degli eventi indipendenti” in questo caso non è valida.
Un’occhiata ai vantaggi
Nel blackjack ogni carta ha un valore specifico che si aggiunge o si sottrae dal vantaggio della casa blackjack che il casinò, appunto, ha nei confronti del giocatore. Quando escono le carte giuste, il vantaggio si azzera o passa, addirittura, a favore del giocatore.
Nel blackjack quando esce un asso o una carta che vale 10 il vantaggio del casinò sul giocatore aumenta. Quando invece vengono messe in gioco carte dal valore più basso, il vantaggio del casinò diminuisce.
E quando sono uscite un numero elevato di carte di basso valore, è il giocatore ad avere un vantaggio sul casinò.
Quando nel mazzo rimangono parecchie carte alte, il giocatore ha un vantaggio nei confronti del casinò e questo succede per diverse ragioni.
Intanto, escono dei blackjack con maggiore frequenza e visto che la vincita sul blackjack non è simmetrica (il giocatore viene pagato 3 a 2, ma perde solo la sua puntata iniziale se fa blackjack il mazziere), questo è un beneficio per il giocatore.
In secondo luogo, alcune delle opzioni del giocatore, come quella di splittare le coppie blackjack o di raddoppiare, aumentano di valore.
Di solito un giocatore vuole vedere uscire una carta alta quando raddoppia o quando splitta una coppia, oppure il giocatore utilizza queste opzioni quando il mazziere è debole e quando è probabile che una carta alta lo faccia sballare.
Questo tipo di giocate ha un ritorno più performante quando il mazzo è ricco di carte alte. E infine, il giocatore può modificare la sua strategia a seconda della composizione delle carte rimanenti.
Con una preponderanza di carte alte, il giocatore può stare con mani più rigide (quelle che vanno dal 12 al 16), raddoppiare a blackjack più spesso con totali forti o quando il mazziere è debole e rischia di andare sopra il 21.
In contrasto, le regole proibiscono al mazziere di variare la strategia a seconda della composizione del mazzo.

All’interno dei numeri
Una strategia che dà un vantaggio dell’1% significa che per ogni mano di blackjack giocata per 100 euro, l’Expected Value è, appunto, pari ad un euro. Questo viene calcolato dall’equazione dell’expected value, l’equazione 1.
EV = DIMENSIONE DELLA PUNTATA (X) % VANTAGGIO (X) # MANI GIOCATE
Equazione 1
Se applichiamo lo scenario dell’expected value al lancio di una moneta, sappiamo che ci sono due lati di una moneta, quindi abbiamo il 50% di possibilità che esca testa e il 50% di possibilità che esca croce, quindi l’equazione che ci dice quante teste ci possiamo aspettare per 100 lanci di una moneta è l’equazione 2.
Si tratta di una equazione a variabile singola e la dimensione della puntata può essere valutata 1.
EV= ½ (X) 100
Equazione 2
Quando una moneta viene lanciata 100 volte, raramente il risultato è di esattamente 50 volte testa e 50 volte croce.
Quindi dobbiamo aggiungere a questo esperimento il concetto di varianza per numero di eventi. La varianza è una misura della dispersione statistica. In termini tecnici, riguarda quanto il risultato di un esperimento si allontana dal valore atteso.
Per rimanere all’esempio del lancio della moneta, la varianza aiuta a rispondere alla domanda se può ritenersi sorprendente oppure no ottenere 45 volte testa in 100 tentativi o ottenere 5 volte testa in 100 tentativi.
Le risposte, lo avete già intuito amici che avete letto il nostro contenuto di matematica applicata al casinò, sono no e sì. Ottenere solo cinque volte testa in 100 lanci di una moneta dimostrerebbe virtualmente che state lanciando una moneta truccata.
Capire questo concetto è fondamentale, poiché per determinare se i risultati (buoni o cattivi che siano) dipendono dalla fortuna oppure dall’abilità, serve, quindi, una giusta analisi statistica.

Un’occhiata alla varianza
La varianza di solito viene discussa in termini di deviazioni standard e sarà così da ora in avanti in questo ragionamento.
La deviazione standard è semplicemente la radice quadrata della varianza. La deviazione standard per una serie di tentativi è data, così, dall’equazione 3.
Deviazione standard = (Deviazione per un singolo evento) X (numero di eventi)^(1/2)
Equazione 3
La figura che segue mostra quanto è probabile che i risultati cadano all’interno di una, due e tre deviazioni standard del risultato atteso.
Nella rappresentazione grafica, il risultato atteso è indicato dalla lettera greca MU, mentre la deviazione standard è rappresentata dalla lettera greca SIGMA.
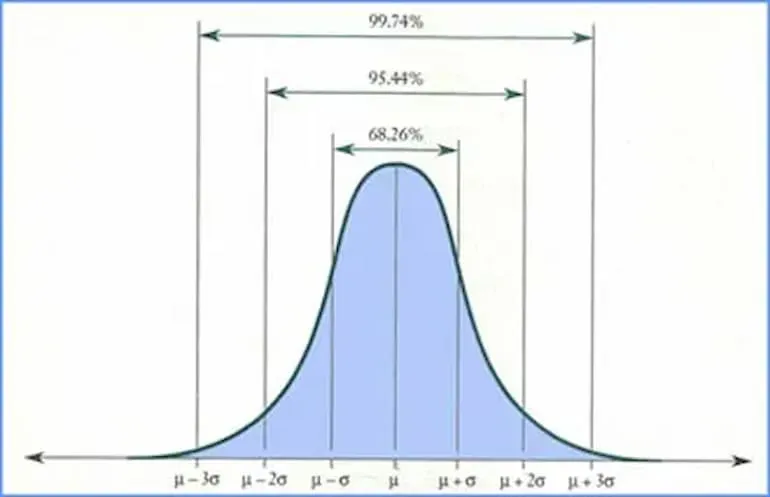
Secondo la curva di distribuzione gaussiana, c’è poco più del 68% di possibilità che il risultato sarà all’interno di una deviazione standard, più o meno del risultato atteso.
C’è poco più del 95% di possibilità che il risultato sia all’interno di due deviazioni standard, più o meno del risultato atteso. C’è quasi il 100% di possibilità che in ogni momento il risultato sia all’interno di tre deviazioni standard.
Come nelle migliori strategie blackjack, applicando questo alla scenario ai 100 lanci della moneta su cui stavamo ragionando in questo paragrafo, concludiamo che la deviazione standard per 100 tentativi è 10 volte la deviazione standard per un singolo tentativo (che è 0,5), il che porta una deviazione standard di 5 per l’esperimento da 100 tentativi.
Nello scenario del lancio della moneta ci aspettiamo che in 50 dei 100 lanci la moneta cada su testa e che in 50 dei 100 lanci la moneta cada su croce.
Includendo il concetto di deviazione standard di già o meno 5, c’è una possibilità del 68% che per 100 lanci di una moneta la moneta in questione cadrà tra 45 e 55 volte su testa e il resto elle volte su croce.
Applicando le equazioni per l’expected value e per la deviazione standard ad un’unità di puntata di 100 euro, con un vantaggio totale dell’1%, ecco che escono i seguenti risultati.
| # di mani | Expected Value | Deviazione standard |
| 100 | 100 | + o - 1.100 |
| 10.000 | 10.000 | + o - 11.000 |
| 1.000.000 | 1.000.000 | + o - 110.000 |
Graficamente, si può anche rappresentarlo come segue.
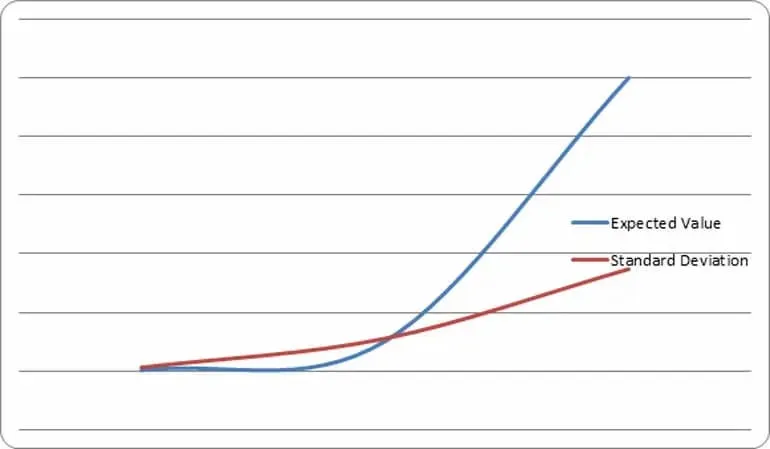
Con l’aumento del numero degli eventi, la deviazione diventa sempre più bassa relativamente all’expected value. In un determinato punto della curva, l’expected value e la deviazione standard si intersecano.
A quel punto c’è una possibilità dell’84% che la deviazione standard sia più bassa dell’expected value.
Questo dà una possibilità dell’84% di fare un profitto. Quando il numero degli eventi aumenta oltre quel punto, la percentuale aumenta in maniera logaritmica. Questo viene illustrato con un’immagine nel grafico che segue.
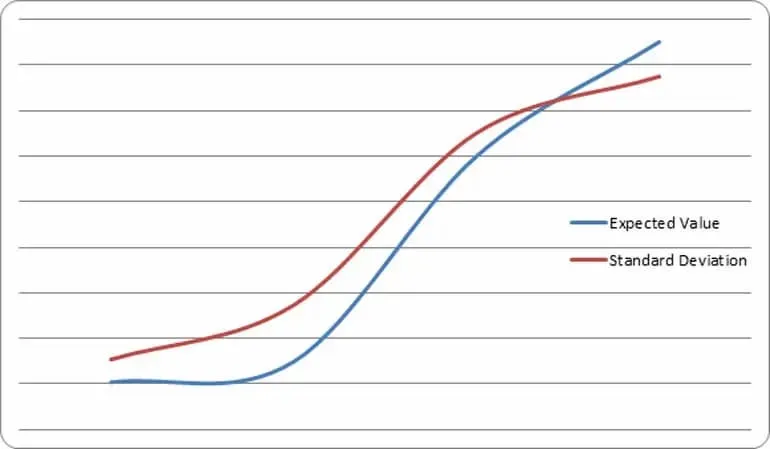
PER SEMPLICITÁ, IL VALORE DELLA DEVIAZIONE STANDARD È ASSOLUTO
Il punto di intersezione tra l’expected value e la deviazione standard è poco sotto le 12mila mani.
A 12mila mani c’è l’84% di possibilità che l’expected value superi la deviazione standard negativa, indicando un EV positivo nell’84% dei casi.
Quando il vantaggio totale è aumentato il punto “di equivalenza”, o il numero di mani in cui l’expected value è uguale alla deviazione standard, si raggiunge con meno mani. Calcolando lo stesso grafico con un vantaggio del 2%, il grafico mostra un punto di equivalenza di 5600 mani.
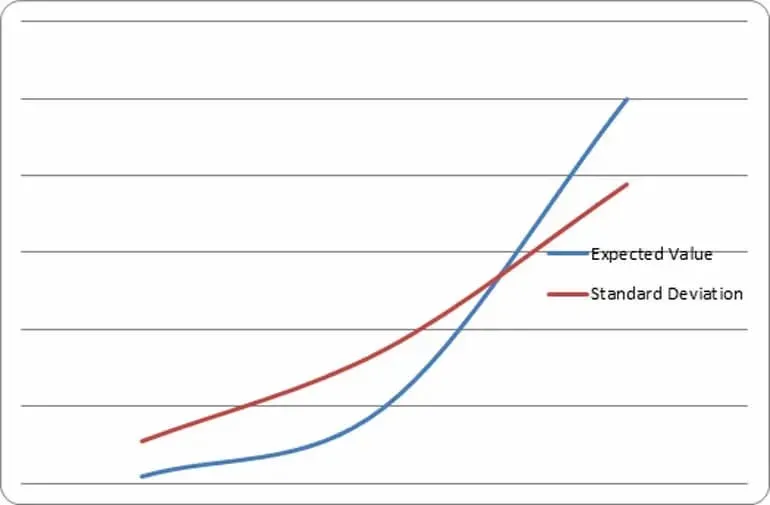
PER SEMPLICITÁ, IL VALORE DELLA DEVIAZIONE STANDARD È ASSOLUTO
Arrivare ad avere un vantaggio
Il modo migliore per conseguire ed approfittare di un vantaggio è avere un’alta diffusione delle puntate. In uno scenario ideale, un giocatore punta molto quando c’è un vantaggio e non punta nulla quando il vantaggio non c’è.
Immaginate un gioco in cui viene lanciata una moneta e quando cade su testa una persona vi paga 2 unità, mentre quando cade su croce siete voi a dover pagare un’unità a quella persona. Giochereste a un gioco del genere? La maggior parte delle persone direbbe di sì.
Ma dovete assicurarvi di avere abbastanza unità da poter superare qualsiasi striscia negativa che potreste incontrare. Se una persona ha solo 4 unità da puntare, è possibile che la moneta cada su croce quattro volte di seguito e che la persona in questione perda tutti quanti i suoi fondi.
Ma se la persona ha 100 unità, avrà abbastanza fondi per superare la striscia negativa nel gioco e c’è un’ottima possibilità che alla fine il gioco al giocatore porti un profitto.
Quando si gioca al casinò, anche al casinò live, servono fondi adeguati per poter superare ogni striscia negativa che può esserci.
In generale, più fondi si hanno, maggiori sono le proprie possibilità di successo. E questo è il motivo per cui i casinò spesso vincono contro i giocatori: perché il giocatore spesso non ha il giusto bankroll per il casinò e, quindi, non è in grado di arrivare a giocare a lungo termine e di superare i dossi statistici che si ritrova ad affrontare.


