In tanti uscendo dal casinò, si chiedono "Perché ho perso?" Questo perché per natura i giochi da casinò hanno un'aspettativa negativa per il giocatore. Ciò significa che per ogni effettuata su un determinato gioco, sia esso un gioco da tavolo o una slot machine, viene restituito meno dell'importo scommesso.
La legge dei processi indipendenti
Valore atteso e deviazione standard
Ad esempio, quando 1 milione di giocatori scommettono 1 euro ciascuno e un solo giocatore vince 500.000 euro, il casinò realizza un profitto di 500.000 e la perdita media per giocatore è di 50 centesimi. Nelle slot machine, come abbiamo già esaminato il payback pubblicizzato è spesso vicino al 97-99%.
Questo è per l'intera vita della macchina, dove una macchina può raccogliere centinaia di milioni di euro nel corso della sua "vita". I giochi da tavolo sono leggermente diversi perché alcuni includono una componente di abilità e, di conseguenza, il vantaggio percentuale del casinò varia da giocatore a giocatore.
Comprendere la matematica al casinò è essenziale per valutare i risultati. Le conoscenze qui condivise sono necessarie per determinare se i risultati, siano essi buoni o cattivi, sono statisticamente accettabili.
Dentro la matematica
Introdurrò la matematica nel casinò, applicando l'analisi al gioco del blackjack. Il blackjack è un gioco di percentuali variabili. E anche se le percentuali cambiano continuamente, la percentuale cumulativa del vantaggio complessivo rimane costante. Ciò si ottiene prendendo la somma dei vantaggi su tutte le possibilità.
Ad esempio, se una mano totale ha un vantaggio del 5% positivo e un'altra mano ha un vantaggio del -4%, allora il vantaggio totale per le due mani è +1%. Quando il lettore comprende questo approccio, è facile tradurre i concetti, mutatis mutandis, in qualsiasi altro gioco con un vantaggio costante sul giocatore, come slot o roulette.
La legge dei processi indipendenti
La maggior parte dei giochi d'azzardo riflette il concetto matematico noto come "legge dei processi indipendenti". Questo afferma che gli eventi passati non hanno alcuna rilevanza sugli eventi futuri. Ad esempio, quando viene lanciata una moneta c'è il 50% di probabilità che il risultato sia testa e il 50% di probabilità che il risultato sia croce.
Se la moneta esce 10 teste di fila, il lancio successivo avrebbe di nuovo una probabilità del 50% di ottenere testa.
Nel blackjack ciò che accade in passato influenza direttamente ciò che accade in futuro. Il blackjack ha memoria e, in questo caso, la legge dei processi indipendenti non è valida.

La tipicità del blackjack
Nel blackjack, ogni carta ha un valore specifico che aggiunge o sottrae valore al vantaggio iniziale che il casinò ha sul giocatore. Il vantaggio iniziale deriva dalle regole del gioco al casino. Quando le carte vengono distribuite, il vantaggio aumenta o diminuisce.
Nel blackjack, quando viene distribuito un asso o una carta di valore 10, il vantaggio del casinò sul giocatore aumenta. Quando vengono messe in gioco carte di valore inferiore (2-7) il vantaggio del casinò diminuisce.
Per determinare l'importo che ci si aspetta di vincere o perdere in un dato momento, sono necessarie tre informazioni chiave:
- Dimensione scommessa
- Numero di mani giocate
- Vantaggio percentuale
In forma di equazione, la dichiarazione recita:
€ vincita prevista = € puntata*% di vantaggio *# mani giocate
Equazione 1
Quando applichiamo lo scenario del valore atteso al lancio di una moneta, sappiamo che ci sono due lati di una moneta, quindi c'è una probabilità del 50% di ottenere testa e, ovviamente, una probabilità del 50% di ottenere croce. Quando scommettiamo 1 euro per lancio, l'equazione per quanto ci aspettiamo di vincere su 100 lanci è:
€50=€1 (scommessa)*0,5% (% di vantaggio)*100(# mani giocate)
Equazione 2
In questo esempio abbiamo, invece, puntato € 100 e vinto 1 euro su 50 di queste scommesse. Siamo stati anche in grado di mantenere la puntata originale di 1 € su 50 di queste 100 puntate. Inoltre abbiamo perso 1 euro su 50 delle scommesse. Questo porta a un gioco a somma zero.
Il concetto di variabilità
Quando una moneta viene lanciata 100 volte, raramente il risultato è esattamente 50 teste e 50 croci. Occorre quindi introdurre il concetto di variabilità per numero di eventi anche per i giochi del casinò. La variabilità, appunto, rappresenta una misura della dispersione statistica. Si tratta, quindi, di quanto lontano dal valore atteso potrebbe essere il risultato di una prova o di un esperimento.
Rimanendo nell'esempio del lancio della moneta, la variabilità aiuta a rispondere alla domanda se sarebbe sorprendente o meno se osservassimo 45 teste su 100 prove, o se osservassimo solo 5 teste in 100 lanci di moneta.
Le risposte sono no e sì. Ottenere solo 5 teste in 100 lanci di moneta dimostrerebbe sicuramente che stavi lanciando una moneta ponderata. Comprendere questo concetto è fondamentale per valutare i risultati dei giochi da casinò, poiché una corretta analisi statistica determina se un giocatore o, addirittura, un casinò viene truffato o meno.

Lo sappiamo, stiamo condividendo ragionamenti ulteriori e complessi, rispetto ai principi su come si gioca a blackjack. La variabilità viene solitamente discussa in termini di deviazioni standard. La deviazione standard è uguale alla radice quadrata della variabilità. La deviazione standard per una serie di prove è rappresentata dalla lettera greca σ (sigma) ed è uguale alla deviazione standard di ciascun evento moltiplicata per la radice quadrata del numero di eventi. L'enunciato matematico si legge come:
σ (totale)=〖σ( evento)*√(Numero di eventi)〗^
Equazione 3
La figura seguente mostra la probabilità che i risultati rientrino in una, due e tre deviazioni standard del risultato atteso. Nella rappresentazione grafica il valore atteso è indicato dalla lettera greca µ e la Deviazione Standard è rappresentata dalla lettera greca σ.
Secondo la curva di distribuzione cosiddetta gaussiana, c'è poco più del 68% di possibilità che il risultato rientri in una deviazione standard, più o meno del valore atteso. C'è poco più del 95% di possibilità che i risultati rientrino in due deviazioni standard, più o meno il valore atteso. C'è, invece, circa una probabilità del 99,9% che i risultati rientrino in tre deviazioni standard in un dato momento.
Applicando questo allo scenario di 100 lanci di una moneta, concludiamo che la deviazione standard per 100 prove è 10 volte (radice quadrata di 100) la deviazione standard per una singola prova (che è 0,5), che produce una deviazione standard di 5 per l'esperimento di 100 prove.
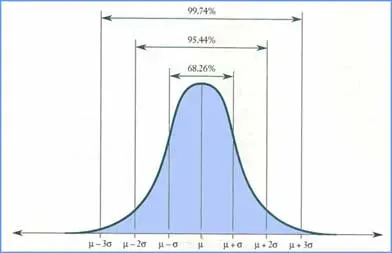
Valore atteso e deviazione standard
Applicando il valore atteso e le equazioni della deviazione standard all'unità di puntata di 100 euro per un gioco da casinò con un vantaggio dell'1% (giocatore o banco) vengono calcolati i seguenti risultati:
|
# eventi
|
valore atteso
|
1σ
|
2σ
|
3σ
|
|
100
|
100
|
+o- 1.100
|
+o- 2.200
|
+o- 3.300
|
|
10.000
|
10.000
|
+o- 11.000
|
+o- 22.000
|
+o- 33.000
|
|
1.000.000
|
1.000.000
|
+o- 110.000
|
+o- 220.000
|
+o- 330.000
|
Graficamente è rappresentato così:
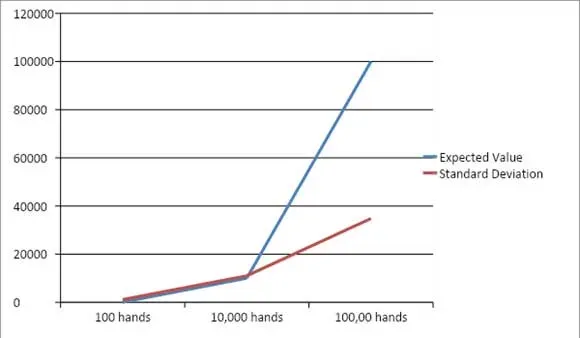
All'aumentare del numero di eventi, la deviazione standard diventa sempre più piccola rispetto al valore atteso. Ad un certo punto lungo la curva il valore atteso e le deviazioni standard arrivano ad intersecarsi.
A questo punto c'è una probabilità dell'84% che la deviazione standard sia inferiore al valore previsto. Ciò significa inoltre che c'è una probabilità dell'84% che da quel momento in poi venga realizzato un profitto e che i tuoi fondi non verranno mai ridotti al punto in cui il bankroll è inferiore ai fondi iniziali. Questo punto di intersezione per una partita con vantaggio dell'1% è mostrato nel grafico seguente.
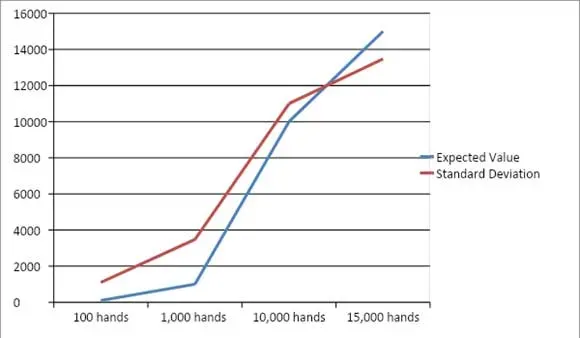
Punto d'equivalenza
Quando il vantaggio complessivo, edge nel blackjack è aumentato il punto di “equivalenza”, ovvero il numero di eventi in cui il valore atteso è uguale alla deviazione standard, viene raggiunto in un minor numero di eventi.
Calcolando lo stesso grafico con un vantaggio del 2% il grafico mostra un punto di equivalenza sostanzialmente inferiore, circa 5.000 eventi.
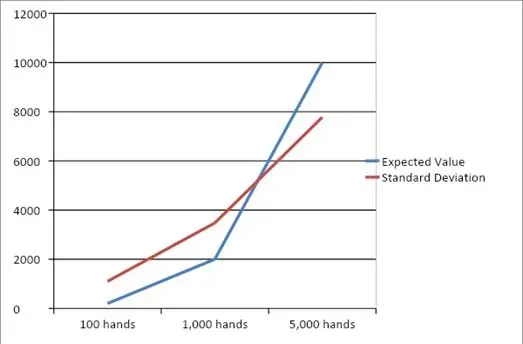
In ultima analisi, i casinò sono in grado di raggiungere il punto di "equivalenza" in modo estremamente rapido.
Questo ha senso perché i casinò live giocano 24 ore al giorno, sette giorni alla settimana. E poiché quasi tutti i giocatori giocano in svantaggio, i casinò guadagnano sempre più soldi con una variazione sempre minore rispetto al loro valore atteso.


