Già l'espressione "calcolo delle probabilità" è un paradosso. Come sosteneva il famoso fisico e filosofo francese alla fine dell'800, infatti: "La probabilità opposta alla certezza è quello che non sappiamo e come facciamo a calcolare quello che non sappiamo?"
Nonostante si parli tanto di matematica applicata al casinò, probabilità e statistica, sembra che siano poche le persone che sanno davvero calcolare in modo algebrico la possibilità di ogni risultato alla roulette.
A volte utilizzano excel o programmi specializzati, cercando di simulare milioni di giri per riuscire a trovare il numero giusto. Quando qualcuno capisce la matematica di base, può rispondere quasi a qualsiasi domanda riguardo la certezza di ogni risultato usando una semplice calcolatrice o inserendo i dati relativi all'equazione come formula in un semplice file excel.
Prima di tutto dobbiamo capire cos'è la funzione fattoriale, che ha come simbolo "!".
Significa moltiplicare una serie di numeri naturali discendenti.
Qualche esempio:
- 4! = 4 × 3 × 2 × 1 = 24
- 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
- 1! = 1
- 0!=1 (assiomaticamente)
In pratica, associandolo alla roulette, il fattoriale mostra in quanti modi differenti diversi elementi (o numeri) possono essere sistemati senza ripetizioni dello stesso elemento o numero.
Per darvi un'idea di quanto possa diventare enorme questo numero, per 37 numeri, come nella roulette europea, è:
- 37! = 1,3763753×1043
Questo significa che ci sono biliardi di diverse sistemazioni dei 37 numeri della roulette, senza contare le possibili ripetizioni dei numeri.
Questo è solo il numero che fotografa in quanti modi diversi (sequenze) tutti i numeri della roulette possono apparire in 37 giri.
L'EQUAZIONE DELLA PROBABILITÀ
Ecco la principale formula matematica per calcolare la possibilità di ogni risultato o evento alla roulette.
Prima di tutto dobbiamo definire i parametri:
P(e) è la probabilità di un evento E;
n è il numero di prove (i giri della roulette);
x è il numero di volte in cui la nostra puntata vince;
P(b) è la probabilità che la nostra puntata B vinca in un giro.
La probabilità P(e) dell'evento E = [Che la puntata appaia x volte in n giri] =
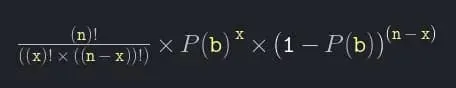
Di nuovo:
P(e) = (n!/(x!(n-x)!)) P(b)x (1-P(b))n-x
Se volete capire questa equazione ancora di più in profondità potete cercare la distribuzione binomiale, che è la base della maggior parte delle probabilità alla roulette.
Voglio anche sottolineare l'importante differenza tra probabilità e aspettativa. Questo è un metodo facile e veloce per calcolare il rischio nella roulette e questo articolo vi aiuterà a capire e a calcolare l'expected value di ogni puntata.
Ora vediamo quanto è potente questo metodo nella pratica. Gli esempi che seguono vi aiuteranno a capire meglio come funziona la formula.
ESEMPI DI PROBABILITÀ SEMPLICE
Poniamo di voler calcolare la probabilità di due numeri Neri in tre giri al casinò. O, per dirla in maniera differente "quanto spesso vedremo esattamente due numeri neri in tre giri".
Notate che questa equazione calcola le probabilità precise di un evento specifico. Non le probabilità di due o più numeri neri, ma esattamente due numeri neri.
I parametri sono:
n = 3 (i giri totali)
x = 2 (i numeri neri / i giri vincenti)
P(b) = 0,5 (la probabilità che esca nero in ogni giro, ignorando lo zero per semplicità)
P(e) = (n!/(x!(n-x)!)) P(b)x (1-P(b))n-x
P(e) = (3!/(2!(3-2)!)) 0,52 (1-0,5)3-2
P(e) = (3!/(2!1!)) 0,52 0,51
P(e) = (3×2×1/2×1×1) 0,25× 0,5
P(e) = (3/1) 0,25× 0,5
P(e) = 3 × 0,125 = 0,375
Quindi, la probabilità che in 3 giri ci siano esattamente due numeri neri è 0,375, o il 37,5%, o poco più di 1/3. Tutti questi numeri sono l'espressione della stessa cosa, l'aspettativa che che l'evento avvenga.
ESEMPIO CON LE DOZZINE ALLA ROULETTE
Vogliamo calcolare la probabilità che una specifica dozzina (non una qualsiasi) esca esattamente 2 volte in 6 giri.
n = 6
x = 2
P(b) = 12/37
P(e) = (6!/(2!(6-2)!)) (12/37)2 (1-12/37)6-2
P(e) = (6×5×4!/(2!4!)) 0,3242 0,6764
P(e) = (30/2) 0,105× 0,209
P(e) = 15 × 0,022
P(e) = 0,329 o 32,9% o circa 1/3
ESEMPIO CON UN NUMERO SINGOLO
Esperti di come vincere al casinò, sapete tutti che nella roulette europea la probabilità che un singolo numero roulette appaia in un giro è di 1/37 o del 2,7%.
Ma qual è la probabilità che un numero specifico esca esattamente una volta ogni 37 giri?

La probabilità che un numero specifico esca esattamente una volta ogni 37 giri è 0,373, o il 37,3%.
Usando la stessa formula possiamo calcolare la probabilità che un numero specifico non appaia in 37 giri (0,362 o 36,2%) e la probabilità che appaia due volte (0,186 o 18,6%).
La formula matematica che abbiamo presentato qui può essere applicata per trovare qualsiasi probabilità per la roulette nella forma "Puntata B che esce X volte in N giri".
UN NUMERO CHE SI RIPETE 3 VOLTE IN 38 GIRI NELLA ROULETTE AMERICANA
Per l'esempio della roulette americana, inserendo i valori nell'equazione principale, otteniamo:

il che significa che la possibilità che ciò accada è 0,06 o 6% o 1/16,6.
Di conseguenza possiamo aspettarci che un fenomeno del genere accada una volta ogni 633 giri. Visto che in 38 giri ha la probabilità di 1/16,6, possiamo aspettarci che avvenga, di media, dopo 38*16,6 = 633 giri
Ecco a voi il link di un modello di un'utile calcolatrice dove potete divertirvi nell' applicare i numeri.


